Newton-Raphson HANK

The sequence-space approach to solving heterogeneous agent models in macro has really opened up some extremely interesting avenues of research. This project implements a Julia-based solution procedure that is essentially a generalization of the Sequence-Space Jacobian (SSJ) method put forward in Econometrica by Auclert et. al. (see here for my Julia-based implementation of that method). The procedure was originally outlined Gregor Boehl’s 2024 working paper, HANK on Speed: Robust Nonlinear Solutions using Automatic Differentiation.

Rapid Iteration

The main drawback to the SSJ approach is that using the methodology requires a pretty intense amount of white-board work before implementing a model in code. In particular, it requires reducing the dimensionality of the model by re-writing the model in the minimum number of variables, matching model “inputs” to model “outputs” by designing a directed acyclical graph (DAG) representation of the model, possibly producing another DAG for the model dynamics—this is a lot of work!

Which isn’t too terrible if you’re working with a single model for an academic paper. But in my capacity as the primary model builder and code developer for the Institute of Macroeconomic and Policy Analysis, I am often working with a whole host of different models and model variants, many of which end up having completely different DAG and minimal-variable representations. And IMPA’s work is still evolving—I expect that we’ll have many more variants in the future. I really needed a flexible solution procedure that is model independent and allows for rapid iteration.

Implementing Newton-Raphson for HANK

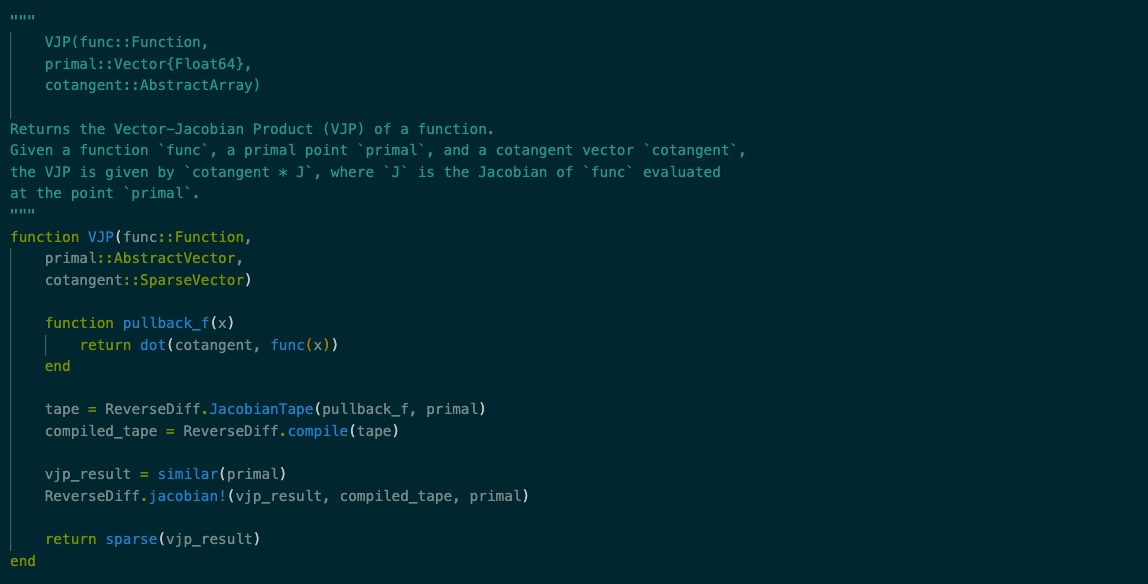
Boehl’s method finds the perfect-foresight solution to a HANK model using the Newton-Raphson method in the sequence space. Most usefully, all we need for this solution procedure is the set of aggregate equilibrium conditions of the model. Thus, it side-steps the whole business of specifying the DAG, reducing the model dimensionality etc.

The usual problem with naively implementing the Newton-Raphson method in HANK models is that the Jacobian is extremely expensive to calculate, making the iterative process very inefficient. The methodology presented in this working paper uses innovations in the automatic differentiation (AD) lietarture to overcome this issue. While the Jacobian itself is expensive to calculate even with AD, AD can compute an intermediary object called a Jacobian-Vector Product (or JVP) very cheaply. Boehl’s method provides a very clever way to iteratively use the JVPs to approximate the Jacobian-related values that the Newton-Raphson method needs. Combined with other advances made in solving HANK models in the sequence space, finding the perfect-foresight solutions even for very large models is impressively fast.

Code

The code repository for my Julia-based implementation of the Newton-Raphson method for solving HANK models is here.

Note that Gregor Boehl has his own Python-based repository that implements this methodology efficiently at EconPizza. The purpose of this repository is two-fold: (1) provide a Julia-based implementation of the basic elements of Boehl’s method, and (2) provide a teaching tool consisting of the basic nuts-and-bolts of this method without the complications that arise when one tries to optimize and generalize the code. (Of course, the real reason is to help me learn how to implement this procedure, but I guess I need an excuse for making this repository public).