IMPA Model

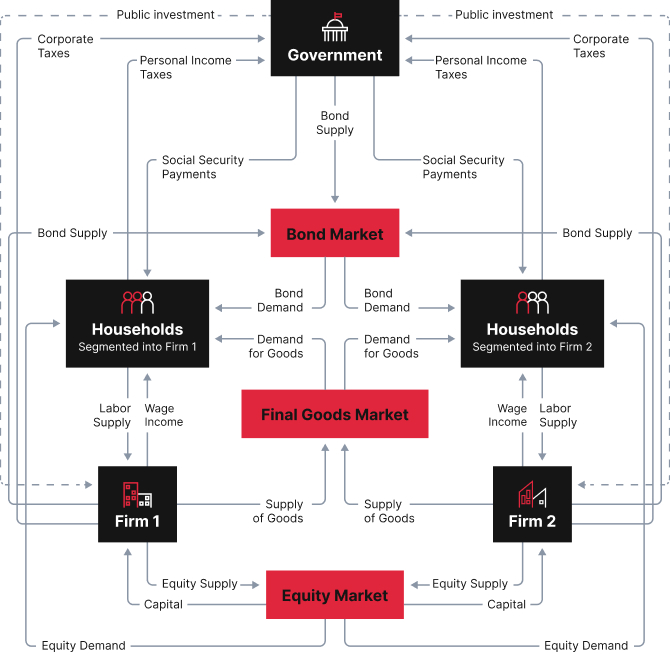
An Overview of the IMPA Model

At the Institute of Macroeconomic and Policy Analysis (“IMPA”), I work on building and extending the IMPA computational model, and using the model to evaluate policy proposals. I am the sole developer of the code base for the computational model, which is a Julia-based implementation of a large scale heterogeneous-agent, multi-sectoral, general equilibrium model of the US economy.

The IMPA model is *large* and involves an enormous amount of complexity and very careful calibration. Among other things, it features:

A Household sector with

• Uninsurable income risk
• Heterogeneity in age, productivity, sector, and wealth levels
• 72 overlapping generations
• Income from wages, stock hodings, and entrepreneurial “pass-through income”
• Savings in bonds and stocks
• Bequests from older to younger geerations

A Government that

• Issues debt
• Imposes payroll taxes and social security taxes on wages, estate taxes on bequests, dividend and capital gains taxes on capital income, and corporate taxes on firms
• Applies progressive taxes (rates and brackets follow the tax code), standard deductions and deductions on pass-through income for households
• Provides deductions on depreciation, interest payments, R&D, as well as investment credits for firms

A production sector with firms that

• Can be either corporate or “pass-through” type
• Can be extended to up to 19 industries/sectors

Building the Computational Model at IMPA

When I joined the Institute for Macroeconomic Policy and Analysis (IMPA), the team had three goals for our computational model: (1) dramatically increase the speed of the model, (2) make the code flexible enough to handle multiple model versions with minimal overhead, and (3) ensure the openness of the code for external review and collaboration.

Days to Minutes

The old MATLAB code base, which followed a simulation-based approach to the solution, was proving to be a bottleneck in our research, limiting the scope of questions we could address.

And so over the last year, I

• rewrote the entire codebase in Julia, which has ended up delivering some pretty amazing speed benefits due to its JIT compiler–loops are as fast as vectorized code!
• moved the model solution to the sequence space following Auclert et al. (2021), which significantly accelerates the solution process for heterogeneous agent models
• incorporated the fastest numerical methods in the game: EGM to get policy functions, Young’s lottery method for transition matrix composition, etc.
• utilized automatic differentiation to compute derivatives quickly while eliminating precision errors. (PS: This needs a separate post by itself some day… AD in Julia, while exciting, is, well, too exciting.)

We’ve seen some pretty remarkable results. A Laffer curve simulation with 17 data points, which took over a day to compute in the old code, now takes just 7 minutes. This means we are able to move faster, try more things, and explore more complex questions without being constrained by computational efficiency.

Leaner, More Nimble Code

The move to Julia brought more than just speed. Julia’s just-in-time (JIT) compilation and multiple dispatch enable functions to adapt dynamically based on input types, reducing code redundancy and making the codebase leaner and more maintainable. Tests are so much easier to write!

I’m also implementing Boehl’s (2024) method for solving dynamics using the Newton-Raphson method. See my post here for a more on why. In a nutshell, this approach decouples the mechanical aspects of solving models from model-specific features, making it much easier to adapt the framework for future models. Once complete, we’ll be able to accommodate new models and variants with minimal adjustments, significantly enhancing our research productivity.

Collaboration

One thing I love about IMPA is it’s commitment to “radical transparancy”. And so I’ve developed the entire codebase on GitHub. The repository is currently private, and will be made public once the testing suite is complete. We’d love for other researchers and practitioners to use, modify and extend our model for their own work.

I’ll share more details here shortly, but in the meantime, you can read more about the IMPA model here.